[백준 1629] 곱셈 (분할 정복, Divide and Conquer)

분할 정복 알고리즘 (Divide and Conquer)

분할 할 수 있는 문제는 분할하고 (Divide) 분할 할 수 있을 때까지 분할 (Conquer)한다.

 

 

백준 1629. 곱셈

1629번: 곱셈

위 문제로 분할 정복 알고리즘이 이런 거구나 하고 이해할 수 있었다.

 

 

문제:

자연수 A를 B번 곱한 수를 알고 싶다. 단 구하려는 수가 매우 커질 수 있으므로 이를 C로 나눈 나머지를 구하는 프로그램을 작성하시오.

 

당연히 보자마자 반복문으로 냅다 돌렸다. ㅎㅁㅎ 결과는? 시간초과 ㅇㅁㅇ !! 이진탐색,, 분할정복,, 으로 혼자 생각해보다가 도저히 아이디어가 떠오르지 않아서 여러 블로그들을 참고했다. 알고리즘을 이해하면서 "분할 정복"이라는 알고리즘을 이해할 수 있었다.

 

 

풀이:

a, b, c 가 차례로 10, 11, 12 로 주어졌다고 가정해보자.

그렇다면 구해야하는 값은 10을 11 제곱한 값에서 12를 나눈 나머지이다. 제곱 수를 분할하여 분할 정복 알고리즘으로 풀어낼 수 있었다.

11 -> 5 * 2 + 1 -> (2 * 2 + 1) * 2 + 1 -> ((1 * 2) * 2 + 1) * 2 + 1

11이라는 제곱 수를 위와 같이 반으로 나눠갈 수 있다. 이를 전체 계산식에 대입하면 다음과 같다.

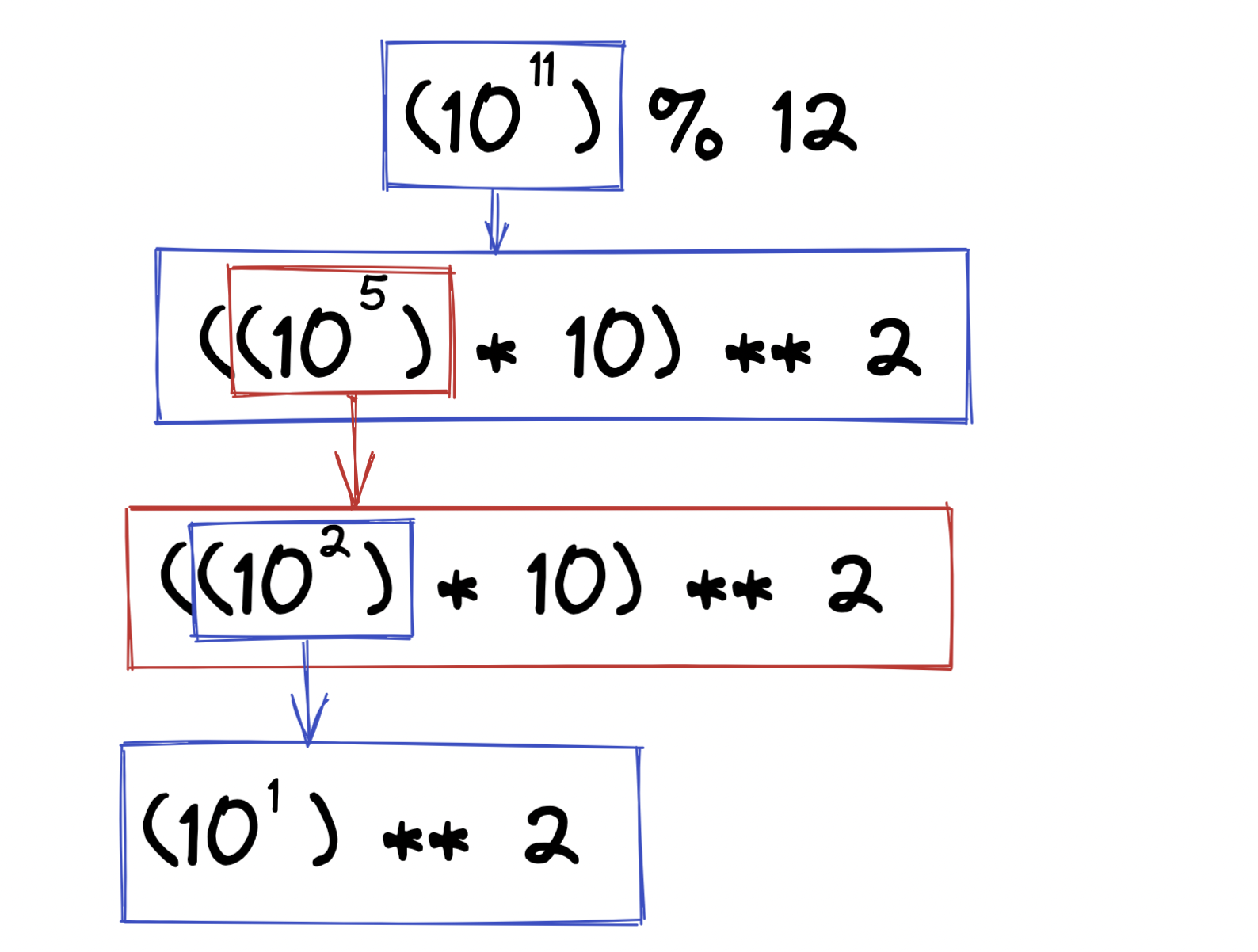
제곱 수를 반으로 쪼개나갔다. 단, 제곱 수가 홀수이면 제곱 수를 반으로 나눈 후, 제곱 대상을 한 번 더 곱해주어야 한다. 같은 방식으로 분할해나가다가 제곱 수가 1이 되면 더 이상 반으로 나눌 수 없으므로 알고리즘 과정이 종료되고, 분할된 식들을 계산한다.

 

위와 같은 식으로 문제를 분할 정복 해가면서 시간 복잡도가 기하급수적으로 줄어드는 것을 확인할 수 있었다. (11번 반복에서 4번 반복)

 

 

코드:

위의 플로우를 코드로 구현하면 다음과 같다.

# 분할 정복
def dac(a, b, c):
  if b == 1:
    return a % c
    
  if b % 2 == 0:
    return (dac(a, b//2, c) ** 2) % c
  else:
    return ((dac(a, b//2, c) ** 2) * a) % c

제곱 수를 반으로 나누어 계산하다가, 1이 되면 계산한 값을 반환한다.

 

 

전체 코드

# 분할 정복
def dac(a, b, c):
  if b == 1:
    return a % c
    
  if b % 2 == 0:
    return (dac(a, b//2, c) ** 2) % c
  else:
    return ((dac(a, b//2, c) ** 2) * a) % c


# 입력 값
a, b, c = map(int, input().split())

# 결과 값
print(dac(a, b, c))

 

 

 

References:

https://developer-next-to-you.tistory.com/35

https://my-coding-notes.tistory.com/93

https://janghw.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Divide-and-Conquer-%EB%B6%84%ED%95%A0%EC%A0%95%EB%B3%B5